It is an attempt to simulate as really as possible a crystal's interatomic interaction under conditions described at main page.

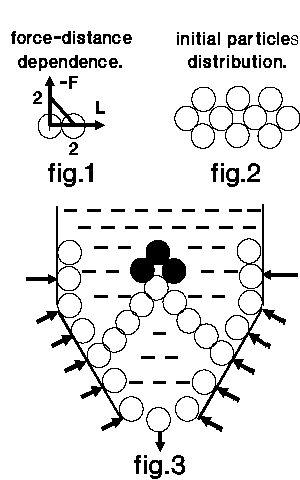Circular particles interact each other by the repulsive central force (fig.1) and are initially distributed at equilibrium distances (fig.2). The arrows (fig.3) show boundary particles movement. Bold elements are motionless and simulate the stopping tip. Most of another particles (simplified by dashed lines) flow free up or down. The particles opportunity to exit down along the axis corresponds to the axial current attenuation (see "one defect" appendix at main page). Intercrystal non-conservative processes were simulated by a force that is equal and opposite to the particle's velocity.

The equations of 2D-motion were solved by simple Euler's method. The method have first order of accuracy, but maximum forces developed in a calculation don't change essentially in the calculation with the time step tenfold bigger. So the calculations give quality and even quantity picture of the system dynamics.

Great concentration of interactions to centre didn't develop at the simulation (only by a factor of 1.5-2). Typical particle configuration, appearing sometimes here, is a chain of particles (fig.3) translating a load from the centre to the boundary almost without its decreasing. It could be caused by "rigidity" of the boundary conditions. A support particle, bound on real crystal surface, steps back under the load, and neighboring particles will take a part of the load. Axially symmetrical geometry also have to give more uniform force distribution.

The most significant result is the several hundred times force multiplication in such configuration compared with free flow forces defined by the frictional processes presence. The flow tendency to "freeze" with big interaction inside confirms the main page description.

Fig.3 gives more effective sample shape than main page one. More close-packed initial particles distribution (than fig.2) decreased the force maximum. These should influence sample's shape and substance. Because the maximum forces don't depend essentially on boundary movement velocity, the effect are statical rather than dynamical.

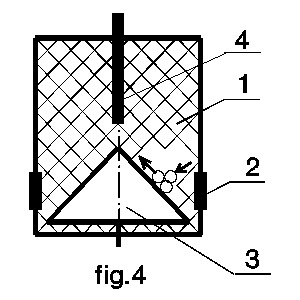One more version of sample (fig.4) could be proposed by the interatomic force analysis. Now forces cumulate along slopes (generatrices) of conical cathode (3). Electric field (order of its atomic value) stabilizes the particles chain on the slopes, and cuts off small force components ^*) that are normal to the cone surface. At a plane normal to the axis, if there are too many particles on a circumference of the cone, a part of the particles step back so that the rest of them will not interact within plain of the circumference.

The dielectric electron conductivity requirement (see main page.) is not valid now. It's unknown whether the stopping element (4) is needful.

^*)- The components are proportional to interparticle intaraction as interparticle distance to radius of the circumference, and if the cathode is a macroscopic object, these forces can be neglected.